環境臭氧,稱為 O 3 ,也稱為地面或對流層臭氧,無論在哪個國家,都會影響地球上的每個人,如右圖所示[1] 。
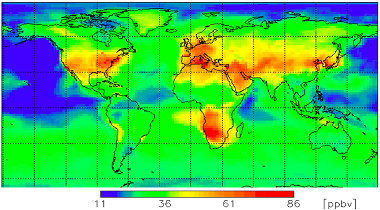
(Attribution: WMO GAW research on reactive gases )
與粒狀物 (PM 2.5 ) 不同,地面臭氧不會直接排放。相反,它是透過在氮氧化物、揮發性有機化合物、陽光和高溫存在下發生的一系列化學反應產生的,如下圖所示:

透過每個國家定義的空氣品質指數標準來量化地面臭氧對健康的影響。有趣的是,世界上一半的國家使用基於毫克的測量標準,而其餘的國家則使用基於 ppb 的測量標準。但這真的是個問題嗎?這就是我們將在本文中討論的內容。
--
美國 EPA 的臭氧標準以 ppm 為單位,而歐洲的臭氧標準以毫克為單位。

因此,我們自然地將問題瞄準了Environnement SA ,這是歐洲領先的環境設備製造商之一,他們開發了自己的O342M臭氧分析儀(見右圖)。
O342M 同時獲得美國 EPA 和歐盟認證(請參閱規格表),因此能夠提供 ppm 和毫克測量。我們向 Environnement SA 提出的問題是「你們的臭氧分析儀如何支援 ppm 和毫克輸出?測量的硬體有什麼區別嗎?如果沒有的話,有沒有轉換的標準? '。
臭氧測量原理
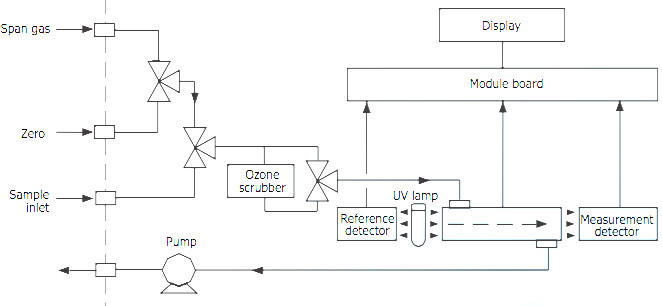
臭氧測量是基於眾所周知的紫外線吸收原理[2] ,即測量臭氧分子的紫外線吸收。臭氧濃度是透過催化轉換器過濾後氣體樣品和不含臭氧的樣品的紫外線吸收率之間的差異來確定的。
在此系統中,臭氧濃度以每體積空氣的光能量來測量,並從中扣除 ppbv 濃度。此系統的可檢測下限為 0.4 ppb(對應於 AQI 0.3,基於美國 EPA 8 小時臭氧標準)。該系統本身並未測量質量,但有一種標準方法可以將 ppmv 轉換為 mg/m 3 。
轉換大氣污染物濃度:從 ppmv 到 mg/m 3
首先,ppm(百萬分之一[3] )和ppb(十億分之一)被定義為“1 ppm = 1/10 6 = 10 -6 ”和“1 ppb = 1/10 9 = 10 - 9 」。因此“1 ppm = 1000 ppb or 1 ppb = 10 -3 ppm”。
轉換係數取決於您想要轉換的溫度(在美國通常為 25 攝氏度)以及環境壓力。在 1 大氣壓的環境壓力下,一般方程式為:
-
c= concentration in mg/m3(i.e., milligrams of gaseous pollutant per cubic meter of ambient air) -
MW= molecular weight of the gaseous pollutant -
ppmv= parts per million by volume (i.e., volume of gaseous pollutant per million volumes of ambient air) -
t= ambient temperature in degrees centigrade. -
12.187= inverse of the Universal Gas Law constant[4]
例如,對於氣態污染物 O 3 (臭氧),要將20 ppmv的臭氧轉換為“25 °C”和1 atmosphere at “mg/m3”,可使用以下公式:
48.00 = `MW(O3)` = molecular weight of Ozone O3. 歐洲和美國轉換標準
對環境溫度和大氣壓力的假設實際上是標準化的,並針對美國、歐洲或正常條件總結在下表中。對於我們的O342M 臭氧分析儀,該係數可由儀器操作員進行使用者編程。
| Gas | Standard Conditions for Temperature and Pressure ( STP) | ||
| "STP US" Conditions at 25°C (US EPA standard) [5] 1013 mbar and 298K | "STP European Union" Conditions at 20°C (EU standard) [6] 1013 mbar and 293K | "Normal" Conditions at 0°C 1013 mbar and 273K | |
| O3 - Ozone | 1 ppb = `1,97` µg/m3 | 1 ppb = `2,00` µg/m3 | 1 ppb = `2,15` µg/m3 |
| NO2 - Nitrogen Dioxyde | 1 ppb = `1,88` µg/m3 | 1 ppb = `1,91` µg/m3 | 1 ppb = `2,05` µg/m3 |
附註:如果有興趣了解為什麼使用 20°C 作為標準參考溫度,可以查看 Ted Doiron 的文章《20°C——工業尺寸測量標準參考溫度的簡史》。
非常感謝來自Environnement SA的 Serge 對臭氧監測儀的快速而準確的答复。請注意,相同的概念也適用於其他氣體,例如二氧化氮(例如使用AS32M分析儀)。
--
為了進一步推動調查,下一個問題是,如果使用實際溫度和壓力而不是參考溫度和壓力,會對計算出的空氣品質指數產生什麼影響?
環境溫度的影響
最後一個問題是研究溫度變化對空氣品質指數的影響。
For instance, let assume that an instrument is measuring an average of `120 mg/m3` of Ozone over 1 hour, which corresponds to an AQI of 50 (Medium) according to the European Common Air Quality Index (CAQI).
在 20°C 和 1 atm 下,`120 mg/m^3` 轉換為 120/2.00,即60.0 ppmv 。因此,我們假設這是臭氧感測器的實際測量值。那麼問題是,如果環境溫度峰值達到 42°C(夏季熱浪期間有時會發生這種情況),那麼正確的質量是多少?換算公式為:
$$c = { ppmv \times 12.187 \times MW \over 273.15 + t } = 111.37 $$
這導致測得的臭氧有「8.6 mg/m^3」的差異。當應用CAQI標準時,相應的AQI為46.4 (而非使用標準20°C條件下的50 )。這實際上是一個可以接受的差異。
右圖總結了根據環境溫度的廣義調整公式。 x 軸是環境溫度,y 軸是計算出的 AQI 是實際溫度,將使用而不是參考溫度 (20°C)。
大氣壓力的影響
至於大氣壓力,變化由理想氣體定律(` PV = nRT` )定義。
值12.187其實是通用氣體定律常數R的倒數。因此,要了解大氣壓力的影響,可以使用以下公式:
換句話說,只需將換算係數除以當前大氣即可。假設壓力p以毫巴( 1 atm = 1013.25 mb )表示,則廣義轉換公式變為:
-
c= concentration in mg/m3(i.e., milligrams of gaseous pollutant per cubic meter of ambient air) -
MW= molecular weight of the gaseous pollutant -
ppmv= parts per million by volume (i.e., volume of gaseous pollutant per million volumes of ambient air) -
t= ambient temperature in degrees centigrade. -
p= ambient atmospheric pressure in millibars.
結論
上述解釋證實了我們最初的假設,即儘管臭氧讀數可以提供不同的單位( ppm和“mg/m^3”),但這實際上不是問題,因為有一種標準方法可以將讀數從“mg/m ”轉換為“mg/m^3” ^3 to ppm`,反之亦然。此外,使用參考STP(標準溫度和壓力)而不是實際環境溫度和壓力的影響是最小的,即,臭氧指數的差異只是單位。
Credits: Ozone visual recreated using Icon pack by Icons8 and taken from American Chemical Society.
